Задачи за крайни автомати

Крайният автомат е абстрактно устройство, способно да установи дали дадена му последователност от елементи (например дума — последователност от букви или морфеми, изречение — от думи и т.н.) принадлежи на определено множество, или не. Автоматът обработва последователността елемент по елемент от начало до край. Във всеки момент той се намира в някакво състояние (състоянията са краен брой — затова говорим за краен автомат), което заедно с поредния елемент определя от кое състояние към кое може да се премине, а буквите до тях — каква буква трябва да „се прочете“, за да се осъществи преходът. Едно състояние е начално — от него започва работата на автомата. Някои състояния са заключителни — ако автоматът се окаже в едно от тях, когато свършат елементите, значи е разпознал последователността като принадлежаща на множеството.

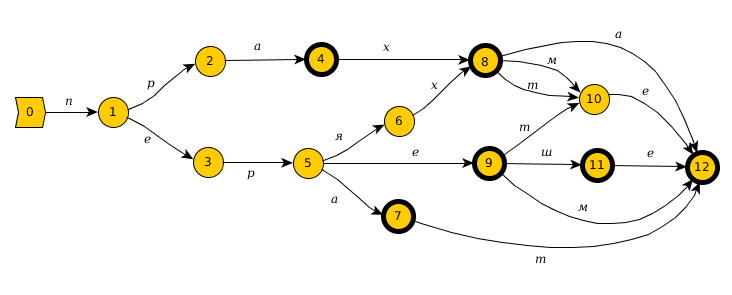
На схемата по-долу виждате краен автомат, който разпознава всички форми на българския глагол пера в сегашно, минало несвършено и минало свършено време. Състоянията са изобразени като възли в графа (с начално състояние и заключителни състояния ); стрелките показват от кое състояние към кое може да се премине, а буквите до тях — каква буква трябва да „се прочете“, за да стане преходът.

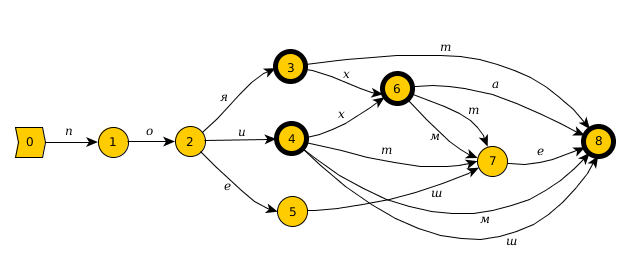
Този автомат разпознава формите за сегашно, минало несвъшено и минало свършено време на глагола поя:

---

Решете следните задачи сами: